---

Test Statistic:

Sample Size:

Test Type: Left-tail (Ha: μ < H0) Right-tail (Ha: μ > H0) Two-tail (Ha: μ ≠ H0)

Significance Level, α: 0.1% 0.5% 1% 2.5% 5% 10% 20% 25% 40%

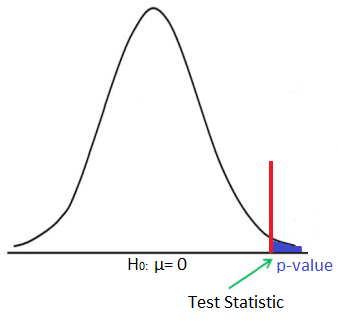
The p-value is a quantitative value that allows us to determine whether a null hypothesis (or claimed hypothesis) is true.

Determining the p-value allows us to determine whether we should reject or not reject a claimed hypothesis.

We set the significance level, which serves as the cutoff level, for whether a hypothesis should be rejected or not. This cutoff point is also called the alpha level (α).

Typical values for the alpha levels are 0.1%, 0.5%, 1%, 2.5%, 5%, 10%, 20%, 25%, and 40%.

If the p-value is less than α, then this represents a statistically significant p-value. This means that we can reject the claimed hypothesis.

If the p-value is greater than or equal to α, we cannot reject the claimed hypothesis.

To calculate the p-value, this calculator needs 4 pieces of data: the test statistic, the sample size, the hypothesis testing type (left tail, right tail, or two-tail), and the significance level (α).

When you're working with data, the numbers of the data itself is not very meaningful, because it's not standardized. You can obtain a whole bunch of data points for a given scenario, but you have to extract meaningful things from it. This is where the test statistic plays an important role.

The test statistic represents the distance between the actual sample results and the claimed value in terms of standard errors. Standard errors is a standardized measure that tells us how far the actual data results obtained are from the claimed data (from the null hypothesis). If the distance between the claimed value and the actual obtained results is small in terms of standard errors, the data is not far from the claim and the chances are the claimed hypothesis (data) is true. If the distance is larger, the actual data shows that we should reject the null hypothesis (H0).

So the test statistic is very important because it gives us a standardized measure that shows how far or close actual results are from claimed data.

The sample size is another variable we need to calculate the p-value. The sample size is very important because it determines whether we use the standard normal distribution (Z-distribution) to look up the p-value or we use the t-distribution to look up the p-value.

If the sample size is less than 30 (n<30), we consider this a small sample size. When the sample size is small, we use the t-distribution to calculate the p-value. In this case, we calculate the degrees of freedom, df= n-1. We then use df, along with the test statistic, to calculate the p-value.

If the sample is greater than 30 (n>30), we consider this a large sample size. When the sample size is large, we use the Z-distribution to calculate the p-value.

This is why the sample size is very important. It determines whether we need to use the t-distribution or the Z-distribution

Next, we must know the hypothesis testing type. This can be left-tail (Ha: μ < H0), right-tail (Ha: μ > H0), or two-tail (Ha: μ ≠ H0) testing.

The hypothesis testing type gives us a frame of reference. If the testing type is right-tail instead of left-tail, then the p-value is, 1- p-value. If the testing type is two-tail, then we need to double the p-value obtained from the test statistic. This accounts for both the left-tail (less than) and the right-tail (greater than) possibilities. This is why it needs to be doubled.

The significance level, α, is the value that we set as the cutoff point for whether we reject a null hypothesis or not. The lower the significance level, the narrower the range we have for accepting the null hypothesis. The higher the significance level, the larger the range we have for accepting the null hypothesis. The most commonly used significance level is probably 5%. This means that if the p-value is lower than the 5% significance level, this means that we can accept the null hypothesis with 95% confidence. If the significance level is 1% and the p-value is lower than this 1%, this means that we can accept the null hypothesis with 99% confidence. If the significance level is 0.1% and the p-value is lower than this amount, this means that we can accept the null hypothesis with 99.9% confidence. If the significance level is 10% and the p-value is lower than this amount, this means that we can accept the null hypothesis with 90% confidence.

So the significance level represents the cut-off point that we choose and determines with what level of confidence we can accept results.

Let's go through a few examples on calculating the p-value.

Suppose that a company claims that the null hypothesis that the average dollar amount that customers spend per transaction is $32 (H0: μ = 32). However, you believe that the average is much less than this (Ha: μ < 32). You calculate that the test statistic is -2.5 based on a sample size of 100 (n= 100). What is the p-value?

The first thing is that this is left-tail hypothesis testing. Because the sample size is greater than 30, it is considered a large sample size. Therefore, we look up the p-value on the Z-distribution table. The test statistic is already given. Looking this up on the chart, you get a p-value of .0062 or .62%.

Another Example: Suppose a company states that they receive, on average, 4 customer complaints a year (μ = 4). However, you had a few terrible experiences with them and believe the actual amount is much greater (μ > 4). Let's say you locate 10 customers (n=10) to find out their experience and obtain a test statistic of 1.96. What is the p-value?

So this is right-tail hypothesis testing. The sample size is 10, so we are going to look up the p-value based on the T-distribution table. Calculating the degrees of freedom, df= 10 - 1= 9. This gives us a p-value of .95. However, since this is right-tail hypothesis testing, to calculate the actual p-value, we must take 1 and subtract this from .95, which gives us a value of .025.

Another Example: Suppose a company states that they receive 200 orders a day but you believe this number is not correct (Ha: μ ≠ 200). You obtain a test statistic of 0.5 based on a sample size of 400. What is the p-value?

So this is two-tail hypothesis testing because the alternative hypothesis is that μ ≠ 200. Because the sample size is large, we look up the p-value on the Z-distribution table. The corresponding p-value is .6915. But we want to find the area beyond this. So we take 1 and subtract the p-value from it. This gives us .3085. Because this is two-tail hypothesis testing, we double this value and get 0.617 or 61.7%.

A point to know is that p-values are probabilities; therefore, they must be between 0 and 1. A p-value greater than 1 or less than 0 represents an erroneous result.

Related Resources

Test Statistic Calculator

Paired t-test Calculator

Unpaired t-test Calculator

T-value Calculator

Expected Value Calculator

Z Score Calculator

Z Score to Raw Score Calculator

Chebyshev's Theorem Calculator

Binomial Coefficient Calculator

Bernoulli Trial Calculator

Area Under the Curve Calculator

Confidence Interval Calculator

Hypothesis Testing Calculator

Sample Correlation Coefficient Calculator

Regression Line Calculator

Slope and y-intercept of a Regression Line Calculator

Sample Size Calculator

Margin of Error for the Sample Mean Calculator

R Squared Calculator (Coefficient of Determination)